Will mathematical extrapolation destroy the world, harm your children, and give you unsightly skin blemishes? Maybe. One of my favorite blogs posted an insightful warning about the dangers of extrapolation. He notes that any number of advancements will, at a macro-level, follow a predictable exponential change that looks like a straight line on a log plot. These relationships can prove surprisingly stable over a period of decades or even centuries; we've been stubbornly doubling transistor counts every 24 months since 1970, for example.

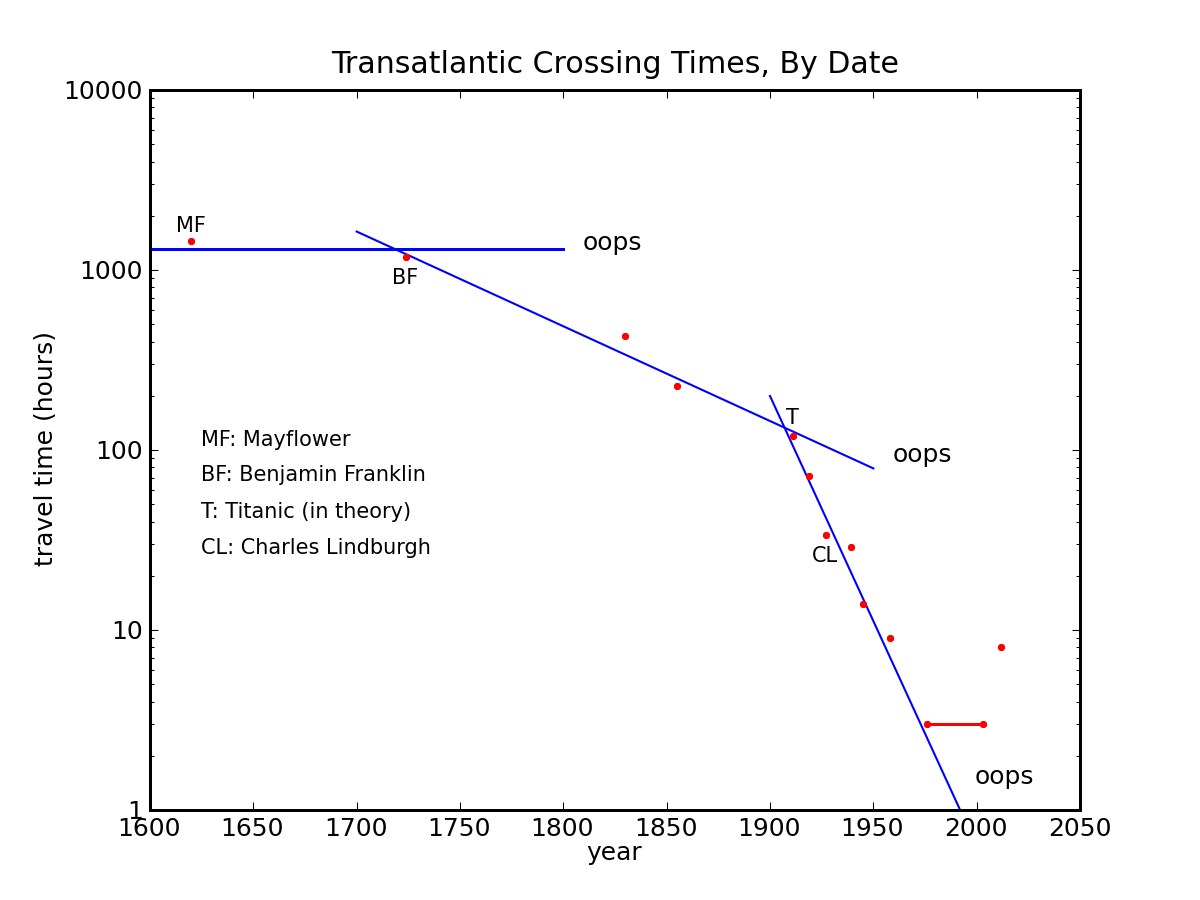
In the world of strategy consulting, the CAGR (compound annual growth rate) is our bread and butter. Read any analyst report on an industry, and predictions for the next 5 years will pretty much just be a rate change inferred from the last 2-3 years. Of course we have more sophisticated tools in our bag. Sometimes we'll plot log production cost versus log units of production. Other times we'll look at technology adoption with a logistic function ("s-curve") or even a bass diffusion model. Hedge funds are constantly plumbing obscure branches of physics or math for models that will give them an edge in modeling predictably irrational market signals. But in the end, humans just expect the near future to be not terribly different than the recent past.

True breakthroughs, game-changers, and disruptions happen much less often than most marketing materials would have you believe. Just because our nice linear models can be broken doesn't mean that we should just throw our hands up and declare the world to be unpredictable. But it does mean that we need to ask yourself what will happen when (not if) our extrapolations will fail. What will break the model? Will your collateralized debt obligation explode if housing prices flatline or drop?

Great post. There are similar instances for ruthless extrapolation on the smaller scale as well. The application of Six Sigma and Design for Six Sigma commonly call for Normal distribution in manufacturing and product development, respectively. However, while the data is tested for Normality, experience lends me to believe that not everything is Normal. Manipulation of the data can be extrapolated to Normal, but that can be, at times, ruthless.
ReplyDelete